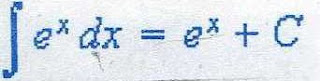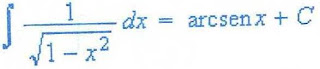DERIVADAS

En geometría, la derivada de una función en un punto representa el valor de la pendiente de la recta tangente en dicho punto. La pendiente está dada por la tangente del ángulo que forma la recta tangente a la curva (función) con el eje de las abcisas, en ese punto.

La derivada de una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje de un plano cartesiano de dos dimensiones. Por ejemplo si tomamos la velocidad de algo, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.

REGLA DE LOS CUATRO PASOS PARA RESOLVER UNA DERIVADA

• Se sustituye la función x·x·Dx,y, se calcula el nuevo número de la función y+Dy.

• Se resta el valor dado de la función del nuevo valor y se obtiene Dy (Incremento de la función).

• Se divide Dy (incremento de función) par Dx (incremento de la viriable independiente).

• Se calcula el limite de esté cosiente cuando Dx (incremento la variable independiente) tiende a cero. El limite así ayado es la derivada buscada.

FÖRMULAS BÁSICAS DE DERIVACIÓN

Dx X= 1

Dx C= 0

Dx UV= UDxV+VDxU

Dx SenU= CosUDxU

Dx CosU= -SenUDxU

Dx CscU= -CscU CotU DxU

Dx SecU= SecU TanU DxU

EJEMPLO:

La fórmula que ocupamos en este caso es la de:

Claro sin olvidar que todas las constantes valen 0 (Dx C=0). Y que "x" vale1 (Dx X =1).

Lo primero que hacemos en esta es multiplicar la "x" con la ecuación para tener solo una

A cada una de los factores le ponemos la derivada

Ahora se deriva

La respuesta es:

INTEGRALES

Integral es una suma de infinitos sumandos, infinitamente pequeños.
Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral

es igual al área de la región del plano xy limitada entre la garfica de f, el eje x, y las líneas verticales x = a y x = b, donde son negativas las áreas por debajo del eje x.

La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada f. En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.

TABLA DE INTEGRALES INMEEDIATAS

Para realizar las integrales son de suma importancia tener a la mano todas las fórmulas:

INTEGRALES

Se dice que cuando una integral de f(X) se puede escribir de la forma f(X)=g(h(x)) h' (x) con g y h' continuas, y se puede hacer el siguiente cambio de variable u= h (x), du=h'(x) y la integral de f(x) cambiarla a la integral de g(u).

La importancia de este método es que una integral que no se puede resolver de forma inmedia al hacer el cambio de variable la transformamos a una integral inmediata.

PASOS PARA LE RESOLUCIÓN DE UNA INTEGRAL POR CAMBIO DE VARIABLE O SUSTITUCIÓN

Tenemos que observar si la integral la podemos resolver por el método directo.
Pero hay que recordar que si la integral esta elevada el cuadrado, al cubo, etc. Seria muy complicado resolverla por el método directo.

• *Así que tendremos que realizarla por el método de sustitución.
  
• *La clave para trabajar con este tipo de integrales es ver que una parate de función al derivar te da la otra parte.
• *Aplicamos el método, la integral se convirtio en una integral directa y por lo tanto aplicamos la fórmula correspondiente para integrala.

• *Una vez integrada la función volvemos a hacer el cambio de variable ya que nustra función depende de "x" y no de "u".

• *Ya obtenemos el resultado.
  
  

EJEMPLO:

1.- Lo primero que hacemos es dividir el problema en factores para resolverlo de una forma mas practica.
2.- En esta caso quedaría así porque solo se divide la secante, porque 6x es una constante que nunca va a cambiar por eso queda igual.

3.-Se aplica la fórmula pero solo a la primera secante.

4.- Después multiplicamos Tangente cuadrado de 6x por Secante cuadrado de 6x y el 1 al igual por Secante cuadrado de 6x.

QUEDARIA

5.- Rompemos nuestro problema en integrales.

6.- Aquí lo que vamos a hacer es ver como esta ubicada , y como podriamos resolver.

Y que otra fórmula podemos ocupar, lo que podemos observar es que (tan 6x) es f(x), por lo tanto lo vamos a derivar.

Vemos que le falta a la ecuación en esta caso seria un 6 antes de "dx" al momento de ponercelo lo tenemos que quitar antes de la integral.

8.- Quedaria de esta forma.

9.-Para poder completar devemos hacer lo mismo con Secante cuadrado de 6x, solo que en esté caso no es f(x) sino es "u" tenemos que sacar "du" y queda de esta manera.



10.-Lo único que nos falto es resolver ahora si directo

NOTA: no se pone secante cuadrado de 6x, por que cuando derivamos es el resultado que nos dio.
Cuando ya sacamos "du" en nuestra segunda integral aplicamos la fórmula para secante cuadrado que seria tan x + C.

Es por eso que queda en el resultado 2 tangentes.

EJEMPLO 2:







* Se divide en integrales





* A plicamos la formula





*Y resolvemos









* Resultado